FİBONACCİ VE ALTIN ORAN

Fibonacci Dizimi ve Altın Oran

1175 yılında İtalya'nın Pisa kentinde doğan bu Matematik dahisi, Matematik ile ilk kez tüccar babasının iş için gittiği Afrika'da tanıştı. Avrupa'da o dönem için Matematikçiler; cadılardan, büyücülerden, tıpla uğraşanlardan daha tehlikeli görülürdü, bu yüzden hoş karşılanmazdı. Fakat Leonardo, Afrika'da Matematik'le tanıştıktan sonra Avrupa'da kullandıkları Roma rakamına dayanan sayı sisteminin yanlış olduğunu, bunun yerine Araplar'ın kullandığı içinde 0 (sıfır) sayısı da olan 10'luk sistemin doğru olduğunu anladı.Çünkü Roma rakamlarıyla işlem yapmak çok zordu.

Bunun birçok sorunu beraberinde getirdiğini düşünerek, 10'luk sayma sistemini Avrupa'ya tanıtmak amacıyla Liber Abaci (Hesap Kitabı) adlı bir kitap yazdı.Kitabın içeriği soyut matematik ve Cebir idi. Leonardo bu kitabıyla Ortaçağ'ın  en ünlü Matematikçisi olmuştur. Çünkü o çağda Avrupa'da Matematikçiler hor görülürken, Arap ülkelerinde insanlar bir şeyler keşfediyor, Avrupa'nın çok sonraları bulacağı birçok şeyi buluyorlardı. (Örneğin; Pascal Üçgeni'ni ilk Ömer Hayyam bulmuştur.)

Fibonacci'yi bu kadar değerli kılan ise, bir problemin çözümü esnasında bulduğu AltınOran'dır.

Bu oran tam olarak

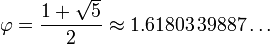
Bu mükemmel oranı bulduran problem ise şudur:

"Dört yanı duvarlarla çevrili bir yere bir çift yavru tavşan konulmuştur. Her çift tavşanın bir ay içerisinde yeni bir çift tavşan yavruladığı, her yeni çiftin de erginleşmesi için bir ay gerektiği ve tavşanların ölmediği varsayılırsa, 100 ay sonunda dört duvarın arasında kaç çift tavşan olur?"

Çözüm ise şöyledir: "1. ay tavşanlar erginleşeceği için yavrulama olmaz. 2. ay bir çift yavru olur. Bundan sonra yavrulamaya başlayan tavşanlar, her ay bir çift  yavru yaparlar. Diğer yavrular erginleşinceye kadar 1 ay geçer. Bu böyle sürerken; 1, 1, 2, 3, 5, 8, 13, 21, ... dizisi ortaya çıkar." Bu dizimde her bir sayı, bir önceki sayıyla toplanarak kendinden sonraki sayıyı oluşturur. Yani; 1+1=2, 2+1=3, 3+2=5, 5+3=8, 8+5=13, 13+8=21, ... olur. Ayrıca bu diziyi bu kadar ilginç ve değerli kılan bir şey vardır. Dizideki her sayının kendinden bir önceki sayıya bölümü yaklaşık olarak Altın Oran'ı verir. Altın Oran, 1.618... şeklinde devam eden bir sayıdır. Bu sayının önemi ise çok  büyüktür. Çünkü evrende bakılan her yerde bu sayıya rastlanır. Örnekleri aşağıdaki  gibidir: Ayçiçeğinde bulunan çekirdeklerin oluşturduğu spiralleri saydığımızda saat yönünde  olanların 55, saatin ters yönünde olanların ise 89 tane olduğunu görüyoruz. Bu iki sayı, yani 55 ve 89, Fibonacci Dizimi'nin birbirini takip eden iki sayıdır ve oranları Altın Oran'ı verir. Çam kozalağında spirallerin sayısı 8 ve 5'tir. Fibonacci Dizimi'nin birbirini takip eden iki sayısı ve oranları Altın Oran'a eşit. Aynı şey tütün yaprakları için de geçerli.   Zambak çiçeğinde 3, düğün çiçeğinde 5, kadife çiçeğinde 13, yıldız çiçeğinde 21, papatyalarda türüne göre 34, 55, 89 tane taç yaprak bulunuyor. Bunların hepsi Fibonacci Dizimi'nin birbirini takip eden sayıları ve oranları Altın Oran'a eşit. Deniz kabuklarındaki spiraller, logaritmik bir şekilde artar. Oranları Altın Oran'ı verir. İkosahedron (12 alt birim beşgen prizmaya sahip, köşelerinden diken şeklinde  uzantılar çıkan yapı.) yapısındaki Adeno virüsünün geometrik şekillerinin oranı Altın Oran'ı verir. Doğadaki bitkilerin yaprakları birbirlerini gölgelememek için belli bir açı yaparak spiral şekilde bir sıraya dizilmiştir. Karaağaç ve ıhlamur ağacı yaprakları 180 derece açı yaparak 1/2, kayın ağacı yaprakları 120 derece yaparak 1/3, elma ağacı yaprakları 144 derece ile 2/5, karaçam ağacı yaprakları ise 5/13 oranı ile dönüş yaparak sıralanırlar. Bunların hepsi, Altın Oran'ı veren Fibonacci Sayıları'dır. [(1, 1, 2 (1+1), 3 (1+2), 5 (2+3), 8 (3+5), 13 (5+8), 21 (8+13), 34 (13+21), 55 (21+34), 89 (34+55), 144 (55+89), 233 (89+144), 377 (144+233), ... (Guy Murchie, The Seven Mysteries Of Life, s. 58-59)] İnsan göbeği ile ayağının arasındaki mesafe 1 birim kabul edildiğinde bir insan boyu  1.618'dir. Parmak ucu ile dirsek arasındaki mesafenin el bileği ile dirsek arasındaki mesafeye  oranı 1.618'dir. Omuz hizası ile baş ucu arasındaki mesafenin baş boyuna oranı 1.618'dir. Göbek ile baş ucu arasındaki mesafenin omuz hizası ile baş ucuna olan mesafeye oranı 1.618'dir. Göbek ile diz arasındaki mesafenin diz ile ayak ucu arasındaki mesafeye oranı  1.618'dir. 1 insanda 2 el vardır. İki eldeki parmaklar 3 bölümden oluşur. Her elde 5 parmak  vardır. Ve bunların sadece 8'i Altın Oran'a göre boğumlanmıştır. Yüz boyunun yüz genişliğine oranı 1.618'dir. Dudak ile kaşların birleştiği yer arasındaki mesafenin burun boyuna oranı 1.618'dir. Yüz boyunun çene ucu ve kaşların birleştiği yer arasındaki mesafeye oranı 1.618'dir. Ağız boyunun burun genişliğine oranı 1.618'dir. Burun genişliğinin burun delikleri arasındaki mesafeye oranı 1.618'dir. Göz bebekleri arasındaki mesafenin kaşlar arasındaki mesafeye oranı 1.618'dir. İnsan akciğerindeki kısa bronşların uzun bronşlara oranı 1.618'dir. Görüldüğü üzere Altın Oran ve Fibonacci Dizimi, doğada her yerde bulunmaktadır. Yukarıda yazdığım örneklerin tüm evrenin çok küçük bir parçası olduğu varsayılırsa, Altın Oran'a neden Altın Oran denildiğini daha iyi anlayabiliriz. Fibonacci bu buluşu ile  aslında yeni bir şeyi keşfetmemiştir. Sadece, doğada zaten var olan düzenin çok  küçük bir parçasını Matematiksel bir yolla insanlığa iletmiştir. Bu büyük dahi, 1250 yılında hayata gözlerini yummuş, ancak insanlığa çok büyük şeyler bırakmıştır. Ayrıca altın oran videosunu izleyebilrisiniz.